Graph representation
Graphs are connections between entities.
- The social network is a graph.
Glossary
| term | definition |
|---|---|
| acyclic graph | a path with no cycles |
| adjacent or incident | when two vertices are connected |
| cycle | a path that reconnects with the origin vertex |
| dag | an acyclic graph |
| degree | the amount of edges between two vertices |
| edge | a line representing the connection between two vertices |
| directed graph | a graph which edges have one direction flow |
| in-degree | the number of edges pointing into a vertex |
| out-degree | the number of edges pointing out of a vertex |
| neighbors | a vertex refering to another adjacent vertex |
| path | the sequential edges that connect two vertices |
| shortest path | the path with less edges |
| sparse graph | graph with relatively few edges |
| to leave | when a directed edge points out of a vertex |
| to enter | when a directed edge points into a vertex |
| undirected graph | a graph which edges go both ways |
| vertex | a single entity |
| vertices | entities in the graph |
Weighted graph
The edges can have a numeric weight.
For example, a weight can be the distance between two cities (vertices).
Use cases
- Social networks
- road maps
- flowcharts
- dependency flow charts
Representation
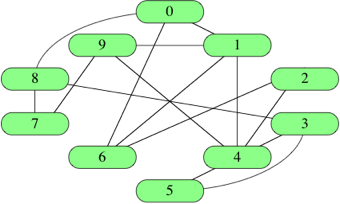
- vertices are mostly names as numbers.
- |V| means all vertices from 0 to V - 1
Criteria
- How much memory or space we need in each representation
- How long will it take to determine whether a given edge is in the graph
- How long it takes to find the neighbors of a given vertex
Types
1. Edge list
An edge list is an array of |E| edges.
- an edge can be an object or a sub-array
- you can add the weight there
Example
const graph = [ [0,1], [0,6], [0,8], [1,4], [1,6], [1,9], [2,4], [2,6], [3,4], [3,5],
[3,8], [4,5], [4,9], [7,8], [7,9] ]
Evaluation
- A search would be more of a linear search unless optimized
- Space is Θ(|E|)
2. Adjacency matrices
A matrix of |V| x |V|
- Symmetric matrix if it is an undirected graph

- The matrix can be represented as an array of rows (sub-arrays)
- The intersections state if there is an edge between x and y
const graph =
[ [0, 1, 0, 0, 0, 0, 1, 0, 1, 0],
[1, 0, 0, 0, 1, 0, 1, 0, 0, 1],
[0, 0, 0, 0, 1, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 1, 1, 0, 0, 1, 0],
[0, 1, 1, 1, 0, 1, 0, 0, 0, 1],
[0, 0, 0, 1, 1, 0, 0, 0, 0, 0],
[1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 0],
[0, 1, 0, 0, 1, 0, 0, 1, 0, 0] ]
Pros
- Search in constant time eg.
graph[1][2]
Cons
- Takes Θ() space
- To determine which vertices are adjacent to a vertex x it takes a linear search through all the x row
3. Adjacency lists
Fusion of Edge lists and Adjacency matrices
- On each row, store only the adjacent vertices to that vertex.
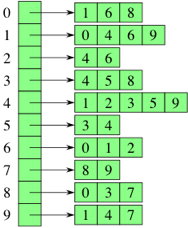
const graph = [
[1, 6, 8], // 0
[0, 4, 6, 9], // 1
[4, 6], // etc...
[4, 5, 8],
[1, 2, 3, 5, 9],
[3, 4],
[0, 1, 2],
[8, 9],
[0, 3, 7],
[1, 4, 7]
];
Pros
- Can get into any vertex in constant time.
- We can find the neighbors in constant time.
Space
- It takes 2 x |V| or Θ(|V + E|) since each vertex is recorded twice in the graph.